文章目录[隐藏]

Few-shot Object Detecion via Feature Reweighting
最近入坑小样本检测,所以会更新一些论文解读,调研一下
本文使用元学习的方法进行训练,基础框架为单阶段目标检测框架(作者提供的代码使用的是yolov2)
建议先了解小样本学习的形式化定义,这里不细讲,由于我最近要写中文论文,所以尽量避免使用英文,base类一律翻译为基础类,novel类一律翻译为新颖类
论文主要提出了两个模块:元学习器和特征重加权模块
- 元学习器:利用基础类的训练数据获取能够用于新颖类的元特征。
- 特征重加权模块:将新颖类的少量支持样本转为一种全局向量,在检测目标物体时用于指明元特征的重要性和关联性
该方法在多数数据集和多种设置下取得了很好的效果,同时良好的迁移性(从一个数据集迁移到另一个数据集)
主要贡献(此处为论文中翻译而来):
- 我们大概是第一个研究小样本目标检测的,这个问题有很好的实际意义但是在小样本学习文献中比图像分类的研究更少
- 我们设计了一个新颖的小样本目标检测模型,该模型可以学习概括性的元特征,还可以通过从少量支持集样本产生特定类的激活置信度来自动重加权用于新颖类检测的特征。
- 我们通过实验证明了我们的模型大幅领先
baseline方法,尤其是标签极度缺少的情况下。我们的模型调整到适用于新颖类明显更快(存疑,和谁比更快,感觉这句话加的有点多余)
整体架构

论文方法框架如图所示,假设有 N 个新颖类需要检测,那么重加权模块需要输入N个类的支持集图片(每个类一张),然后将其转换为N个重加权向量,每个向量负责从对应类别中检测新颖类目标。整个训练过程分为两步:
- 在基础类上训练
- 在新颖类上微调
特征重加权
作者将整个模型分为三部分:
- 元特征学习器
D
\mathcal D
D:采用YOLOv2的骨干网络(DarkNet-19) - 重加权模块
M
\mathcal M
M:轻量级的CNN,文中由于篇幅限制放在了附加材料中。 - 检测预测模块
P
\mathcal P
P:YOLOv2的回归和分类部分
该模型的形式化流程定义: - 设查询样本(图片)为
I
I
I - 将
I
I
I输入到D
\mathcal D
D得到元特征输出F
∈
R
w
×
h
×
m
F \in \mathbb R^{w\times h\times m}
F∈Rw×h×m,即F
=
D
(
I
)
F = \mathcal D(I)
F=D(I),该元特征有m
m
m张特征图(通道数为m
m
m) - 标记
I
i
I_i
Ii为支持集图片,M
i
M_i
Mi为对应的图片上第i类的目标物的协助标注(有目标的位置为1,无目标的位置为0的单通道掩码图),其中i
i
i代表类别,且i
∈
[
1
,
⋯
,
N
i \in [1, \cdots, N
i∈[1,⋯,N - 重加权模块
M
\mathcal M
M的输入为(
I
i
,
M
i
)
(I_i, M_i)
(Ii,Mi),将其编码为第i
i
i类的特征表示w
i
∈
R
m
w_i \in \mathbb R^m
wi∈Rm,即w
i
=
M
(
I
i
,
M
i
)
w_i = \mathcal M(I_i, M_i)
wi=M(Ii,Mi) - 将元特征
F
F
F与第i
i
i类的重加权向量融合得到第i
i
i类的元特征,公式为:
F
i
=
F
⊗
w
i
,
i
=
1
,
⋯
,
N
F_i = F \otimes w_i, i = 1, \cdots, N
Fi=F⊗wi,i=1,⋯,N
其中⊗
\otimes
⊗表示通道维度相乘(注意F
F
F的通道数和w
w
w的维度相同,都是m
m
m),这里作者是通过1
×
1
1\times1
1×1的深度维度卷积实现的。 - 将
N
N
N个F
i
F_i
Fi输入到预测模块P
\mathcal P
P中得到位置回归得分o
o
o,位置(
x
,
y
,
h
,
w
)
(x, y, h, w)
(x,y,h,w),以及分类得分c
c
c,具体公式为:
o
i
,
x
i
,
y
i
,
h
i
,
w
i
,
c
i
=
P
(
F
i
)
,
i
=
1
,
⋯
,
N
{o_i, x_i, y_i, h_i, w_i, c_i} = \mathcal P(F_i), i = 1, \cdots, N
oi,xi,yi,hi,wi,ci=P(Fi),i=1,⋯,N
其中c
i
c_i
ci表示对应目标物属于第i
i
i类的概率。
学习策略
论文介绍了具体的元学习学习策略(就是将一个大任务,拆成多个小任务,每个小任务抽取一部分支持集,一个查询样本训练,然后不断重复)。论文奖整个训练过程分为两个部分:
- 第一部分使用基础类数据训练
D
\mathcal D
D,M
\mathcal M
M,P
\mathcal P
P; - 第二部分同时使用基础类和新颖类数据进行微调,此时,基础类和新颖类都只使用
k
k
k个样本训练,其余部分与第一阶段相同。 - 在推理部分,论文将微调部分每个类的
k
k
k个样本的重加权向量求平均作为该类的重加权向量,所以,推理阶段只需要输入查询样本,并且重加权模块M
\mathcal M
M可以删除。
检测损失函数
作者发现使用简单的二值交叉熵会导致多余的结果(例如,把火车检测成公交车或者汽车),这是因为一个区域应该只有属于
N
N
N个类中的一个目标物是真正的正样本
- 这里感觉作者解释的有点不清楚,我的理解是,最终的分类得分
c可能有几个类都很高,但是我们需要的只有一个,这时很可能出现错误
作者设计了softmax层解决这个问题。将分类得分
c
c
c进行进一步计算,抑制错误类的得分,得到第
i
i
i类的真正得分
c
^
i
=
e
c
i
Σ
j
=
1
N
e
c
j
\widehat c_i = \frac{e^{c_i}}{\Sigma^N_{j=1}e^{c_j}}
c
i=Σj=1Necjeci。
训练过程分类得分的最终损失函数为:
L
c
=
−
Σ
i
=
1
N
1
(
⋅
,
i
)
l
o
g
(
c
^
i
)
\mathcal L_c = -\Sigma^N_{i=1}{\mathbb 1(\cdot, i)log(\widehat c_i)}
Lc=−Σi=1N1(⋅,i)log(c
i)
其中
1
(
⋅
,
i
)
\mathbb 1(\cdot, i)
1(⋅,i)是指示函数,当前目标框真正属于当前类别时等于1,否则为0。
其余loss与YOLOv2大致相同,只是去掉了一些负样本的损失。
重加权模块输入
输入时将RGB图像加入一个维度mask维度,该维度在有目标物的部分为1,其余为0。如果一张图片有多个目标,只选择其中一个。
实验
数据集
- VOC:VOC07的测试集用于测试,VOC12和VOC07的训练验证集用于训练,一共20个类,随机抽取5个类作为新颖类,生育15个类作为基础类,评估了3种不同的划分。实验取
k
=
1
,
2
,
3
,
5
,
10
k = 1,2,3,5,10
k=1,2,3,5,10 - MS-COCO:使用验证集的5000张图片作评估,训练集和验证集的剩余样本用于训练,一共80个类,选择与VOC重复的20个类作为新颖类,其余作为基础类。
- 还实验了将COCO的60类作为基础类,将VOC的20类作为新颖类的实验,记为COCO to PASCAL
- 测试集可能有基础类的目标物(不用检测的),还有一些图片不含目标新颖类的目标物,使得识别很难。
基准
- YOLO-joint:YOLOv2框架;同时使用基础类和新颖类进行训练
- YOLO-ft:YOLOv2框架;使用基础类训练,使用新颖类微调,同样迭代次数。
- YOLO-ft-full:YOLOv2框架;使用基础类训练,新颖类微调,完全收敛。
实验效果
-
VOC

-
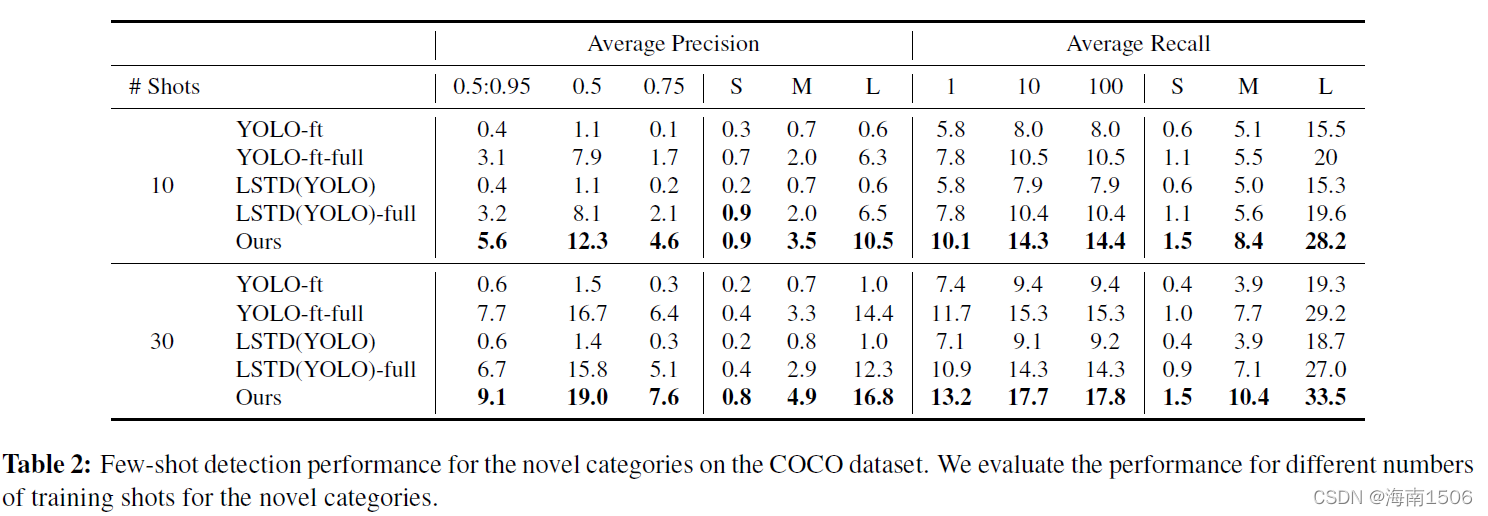
COCO
-
学习速度

-
重加权置信度可视化

-
元学习比直接训练在基础类的效果

消融实验
-
哪一层的特征用于重加权

-
不同的损失函数

-
重加权模块的输入

版权声明:本文为CSDN博主「海南1506」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_44340538/article/details/122224110









暂无评论