高光谱目标检测论文学习（2）——OSP Using Data Sphering and LRaSMD for HTD

文章目录[隐藏]

前言
思路
Data Sphering OSP
LRaSMD OSP
DS与LRaSMD结合的OSP
3D-ROC
总结

前言

这篇论文的原题目叫《Orthogonal Subspace Projection Using Data Sphering and Low-Rank and Sparse Matrix Decomposition for Hyperspectral Target Detection》，与高光谱系列（1）中的论文出自同一作者。这篇论文主要是对高光谱目标检测领域一个非常经典而著名的方法OSP（正交子空间投影）进行了改进，和上篇文章的方法内容有相似之处。

思路

我们知道OSP方法是一种非常经典的高光谱目标检测方法，其最先提出是被用于数据降维，后面才被引入到了混合像素的高光谱目标检测中。
在上一篇文章中，我们提到，OSP方法被用于如下所示的模型：
在这里插入图片描述
OSP的作用是在

[

]

M=[m_1,m_2,...,m_p]

$M = [m_{1}, m_{2}, . . ., m_{p}]$ 中把我们感兴趣的目标特征

m_p

$m_{p}$ 提取出来，而将其余的特征全部都抑制掉，因此引入了一个正交子空间投影器，定义如下：
在这里插入图片描述
其中

[

−

]

U=[m_1,m_2,...,m_{p-1}]

$U = [m_{1}, m_{2}, . . ., m_{p - 1}]$ ，即为不感兴趣的目标特征矩阵，U^#为U矩阵的伪逆。之后用匹配滤波的思想构造检测器：
在这里插入图片描述
其中

d^T=m_p

$d^{T} = m_{p}$ ，表示感兴趣的目标特征，后面括号里的内容就是用OSP处理后的目标特征矩阵。
也就是说，OSP的过程实际上就是首先通过一个投影算子来抑制背景信息，然后再进行目标检测，这个抑制的过程依靠的是U矩阵。

通过分析上述的过程，我们可以很自然的发现这种检测方法的问题：对先验知识太过敏感，我们需要完整获取U矩阵才能有不错的效果，而实际情况中的背景信息往往是未知的。
那么我们就想如何去通过别的手段来表示背景信息呢？这里作者给出了两个方法。

第一个方法借鉴了CEM方法，其核心思想是用二阶统计量去表示背景，最后再将二阶统计量消除以达到抑制背景的效果。CEM通过计算相关矩阵的逆矩阵R^-1来抑制由R表征的背景信息。
第二个方法则是通过一种叫低秩稀疏矩阵分解（LRaSMD）的思想，采用GoDec算法具体实现分解，把样本数据X拆分成X=L+S+N三个矩阵。其中L矩阵为低秩矩阵，表示背景信息；S矩阵表示稀疏矩阵，表示目标信号信息；N为噪声矩阵，表示数据扰动。

基于以上两种表示背景信息的方法，作者给出了三种对OSP的改进方案。
第一种方法叫Data Sphering。这种方法选用了一阶统计量均值和二阶统计量协方差来表示背景，通过消除这两个量来抑制背景。
第二种方法采用LRaSMD中的GoDec将矩阵分解成三个矩阵，用L矩阵表示背景，S矩阵或S+L矩阵表示目标子空间，因此就可以用L矩阵去代替U（此时算子

P

1

U

P_{\frac{1}{U}}

$P_{\frac{1}{U}}$ 变为

P

1

L

P_{\frac{1}{L}}

$P_{\frac{1}{L}}$ ），用S或S+L代替d。
第三种方法就是把第一种和第二种结合起来，既用Data Sphering也用LRaSMD。

最后为了更好的评估性能，提出了我们在上篇文章种简单分析过的三维ROC曲线来代替二维ROC曲线。

Data Sphering OSP

这个方法基本上就是我们前一篇文章中提到的DS-space空间白化方法，因此这里仅作简单阐述。
DS的变化形式如下所示：
在这里插入图片描述
本文没有给出DS的具体变化，因此我们直接用了另一篇论文中的表示，通过上面的变化，我们可以知道，对原始数据空间中的特征作DS就相当于是对一个特征先通过减法去掉一阶的均值特征

\mu_b

$μ_{b}$ ，再通过乘法去掉二阶的协方差特征

−

K^{-1/2}

$K^{- 1 / 2}$ 。因此我们用DS变换后的

\hat{d}

$d^$ 和

\hat{U}

$U^$ 来代替原来的d和U。
因此变换后检测器可以写作：
在这里插入图片描述

LRaSMD OSP

GoDec算法

首先我们来介绍一下LRaSMD方法和GoDec算法。
我们知道LRaSMD方法的的本质思路是把一个矩阵分解为低秩矩阵和稀疏矩阵相加的形式，因此，如何表示其中的低秩矩阵和稀疏矩阵就成为一个很关键的问题。
在最初的一种分解方法RPCA中，我们分解为

X=L+S

$X = L + S$ ，即只有两部分组成，这种分解方法是吧噪声算到了S矩阵中，因此采用如下PCP方法去解决噪声问题，并求解矩阵：
在这里插入图片描述
之后，在RPCA的基础上，受到压缩感知和随机矩阵估计的思想的影响，GoDec方法产生了。
我们重新对矩阵X进行分解，分解为：

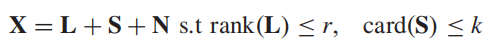
这个时候发现引入了N矩阵作为噪声矩阵，表示数据扰动，此时的S矩阵就是一个纯粹的稀疏矩阵S了。
对于上面这个式子，我们可以通过最小化分解误差来求解，即转化为一个优化问题：
在这里插入图片描述
rank为矩阵的秩。cardinality为矩阵的基数，用来表征矩阵中元素的个数。

∣

∣

⋅

∣

∣

F

||·||_F

$∣ ∣ \cdot ∣ ∣_{F}$ 表示Frobenius范数，定义为矩阵各项元素的绝对值平方的总和开根，即：
在这里插入图片描述
为了求解这个优化问题，我们可以拆分成两个子问题：

此时L和S可以通过互相迭代求解，类似于围棋中的双方博弈，这也是算法名称中“Go”的由来。
具体来说，

L_t

$L_{t}$ 可以通过

−

X-S_{t-1}

$X - S_{t - 1}$ 的奇异值硬阈值（前r个奇异向量）更新；

S_t

$S_{t}$ 则可以通过

−

X-L_{t-1}

$X - L_{t - 1}$ 的entry-wise 硬阈值（数值从大到小排列前k个元素组成的非零子集）更新。

但是奇异值分解（SVD）这个方法太耗时了，因此考虑用双边随机投影（Bilateral Random Projection，BRP）来计算。

我们对输入的X矩阵作双边随机投影，分别投影到列空间

Y_1=XA_1

$Y_{1} = X A_{1}$ 和行空间

Y_2=X^TA_2

$Y_{2} = X^{T} A_{2}$ ，其中A1和A2都是随机矩阵。因此低秩矩阵L就可以表示为：
在这里插入图片描述
此时我们看出，这个矩阵的计算已经比作奇异值分解要简单很多了。

我们还可以使用Power Scheme进一步对模型进行优化，减少矩阵X奇异值衰减缓慢的影响。重新定义一个用于替代X的矩阵：
在这里插入图片描述
这里的q就是Power Scheme参数，用来提高近似精度，可以通过增加q值来使减小L矩阵的误差。
特别的，

(

)

(

～

)

\lambda_i(X)=\lambda_i(X^～)^{2q+1}

$λ_{i} (X) = λ_{i} (X^{～})^{2 q + 1}$ ，其中

\lambda_i

$λ_{i}$ 为矩阵的第i个最大奇异值。
那么上面的L就变成：

～

(

)

−

L^～=Y_1(A_2Y_1)^{-1}Y_2

$L^{～} = Y_{1} (A_{2} Y_{1})^{- 1} Y_{2}$

之后我们为了获取X对应的低秩矩阵L，对Y1和Y2矩阵作QR分解，QR分解的定义如下：
在这里插入图片描述
得到如下形式：

这个L是由

～

L=L^{～\frac{1}{2q+1}}

$L = L^{～ \frac{1}{2 q + 1}}$ 推导得来。
最后得稀疏矩阵S为：
在这里插入图片描述

(

⋅

)

P_{\Omega}(·)

$P_{Ω} (\cdot)$ 表示元素集Ω对矩阵的采样投影，Ω为|X-L|的前k个最大元素非零子集。

总结一下，GoDec算法流程如下：
在这里插入图片描述

用低秩矩阵L的OSP消除背景

我们进行目标检测首先要做的一件事，是把背景给抑制掉，从而突出目标，因此这一部分首先先来看看怎么用OSP消除背景。
定义消除背景的投影算子为：
在这里插入图片描述
B就是表示背景的矩阵。那么检测器就可以写作：

在前面我们提到过，低秩矩阵L就可以用来表示背景信息，因此B=L，所以，有：

用稀疏矩阵S的OSP检测目标

上面的OSP只用到了低秩矩阵L，而没有用到我们分解出的稀疏矩阵S。当我们用L去除掉了背景之后，剩下的S就可以看作是有用的目标信息了，因此，我们可以在现在这个包含有目标信息的子空间中再去找d和U两个量。因此，检测器可以重新定义为：
在这里插入图片描述
可以看出背景信息被L-OSP抑制；这里的

d_S^T

$d_{S T}$ 和

⊥

P_{U_s}^⊥

$P_{U_{s} ⊥}$ 就是在S生成的子空间中获得的d和U。

用S+L的OSP检测目标

这里还给出了一种用S+L两个矩阵的OSP去检测目标的方法，这种方法基于目标信息也可能嵌入到背景中这一可能性提出。这个时候检测器定义为：
在这里插入图片描述

DS与LRaSMD结合的OSP

文章还把上面两种方法结合起来又进行了实验，这一部分的本质其实就是在做方法的排列组合，没有特别新颖的想法，因此作简单阐述。
第一种结合方法是：把L-OSP的原始数据空间进行DS，称作L-DSOSP。
因此检测器为：
在这里插入图片描述
第二种结合方法是：在第一种方法的基础上把L矩阵也进行DS，记作L^-DSOSP。
因此检测器为：

第三种方法是仅对L矩阵DS，其余的仍沿用(L,S)-OSP，记作(L^,S)-OSP。
因此检测器：

第四种方法是仅对S矩阵DS，其余的沿用(L,S)-OSP，记作(L,S^)-OSP。
因此检测器为：
在这里插入图片描述
第五种方法是对S和L都进行DS，并套用(L,S)-OSP，记作(L^ , S^)-OSP。
因此检测器为：

第六种方法是只对L+S进行DS，并套用(L,S+L)-OSP。

第七种方法是对L+S和L都进行DS并套用(L,S+L)-OSP。

到目前为止，文中给出了如下11种检测器：
在这里插入图片描述