文章目录[隐藏]

前言
从这篇开始,将会学习一些高光谱目标检测的论文,我仍然把这篇文章放到了读论文专栏里,但是不对其进行顺序编号了,因为这个方向是比较小众的。今天来学习这篇TGRS2021的最新论文,讲的比较详细,相对比较适合初学者入门。我之前也写过一些有关目标检测的论文,但是高光谱目标检测(HTD)和之前的我们学的目标检测是不同的,因为其检测的对象不是普通摄像头得来的数字图像,而是高光谱遥感图像。其包含了很多光谱信息,而光谱信息本身经过处理后就可以作为特征,因此很多情况下就无需使用广义的目标检测问题中的卷积神经网络等方式去提取特征,而且通常来说,光谱特征可以直接反应一种物质的种类,因此也无需自己去进行学习与分类。因此,这个问题就退化为了一个分类问题。我们再对问题作简化,简化为一个二分类问题,即只需研究对于某种目标,给定的像素中存不存在该目标。那么问题就进一步退化为了:将一个待考察像素判定为目标或者非目标的二元假设检验问题。
思路
我们首先来具体阐释一下高光谱目标检测的原理:
高光谱图像的各波段在成像范围内都是连续成像,因此高光谱的光谱曲线一般是平滑的、连续的曲线。高光谱图像的波段中涵盖了物质的光谱信息,而每种物质的光谱信息都不一样,我们可以利用图像像素的光谱波段所包含的特定的光谱信息来判断该像素所代表的特定的物质种类。
那么如何作高光谱目标检测似乎已经浮出水面了,我们只需要提取目标物质的光谱特征,利用这个特征做一个用于检测的函数,然后把待检测像素的光谱特征提取出来,代入这个检测函数中,通过设定阈值或其他判断方法,就可以判断这个像素是不是属于目标物质。
因此,我们可以把高光谱目标检测(HTD)问题看作是:
在高光谱遥感图像的每个像素中寻找某种目标物质的存在性问题。
再抽象且数学化一点就是:
将一个待考察像素判定为目标或者非目标的二元假设检验问题。
这种抽象建模的方式就是文章介绍的第一种思想——假设检验,具体到方法就是基于假设检验的LRT(似然比检验,likelihood ratio testing)方法。
这种方法有什么弊端呢,我们回顾一下概率论与数理统计课程中学过的似然比检验:
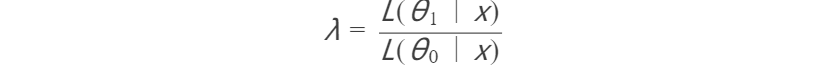
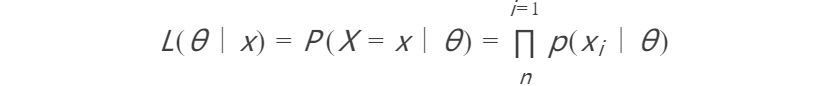
可以知道,采用LRT方法时需要一些先验知识,尤其是一些先验概率分布的特征,以往的方法都会对背景或噪声的概率分布做高斯假设,但是实际上由于数据中本身存在一些细微物质或者干扰,高斯假设并不是在任何情况下都能取得较好的效果。那么我们能不能避开高斯假设呢?
答案是可以的。这就是本文用到的第二种方法,基于SNR的检测理论。这种方法其实本质上就是把进行检测的准则由多元高斯分布建设下的LRT变成了信噪比,其基本思想其实就是做了一个线性的匹配滤波。这样的好处是,无需对背景和噪声的分布进行高斯假设,而是只需要简单假设背景与信号不相关即可。但是实际上基于SNR的检测理论也是在最后回归了第一种方法,只不过是用SNR的方法重新推导了LRT形式的检测,实现了两种理论的统一。有关SNR检测的理论之前也有人提出过,名为CEM算法,本文将这个前人的方法与自己的理论做了一个统一。
为了配合SNR-based的HTD方法,作者提出了三种数据白化的方式——DS、协方差矩阵K-数据白化和自相关矩阵R-数据白化。所谓数据白化,其实就是对数据做了去相关处理后再归一化处理,在HTD中,白化主要是为了通过关联二阶数据统计等方式来去除背景的影响。有关细节在后面部分阐释。
除了基于SNR的方法,本文还提出了一种基于SA(光谱角)的方法,这里的主要思想还是滤波的思想,只不过是把线性的匹配滤波器变成了非线性的,而最简单的非线性滤波器就是去测量两个光谱向量之间的角度,因此就有了基于SA(光谱角)的方法。
文章在谈完这三类方法之后,还给出了一种新的评估手段,即将原来的二维ROC曲线改为了三维的,这样就能更好的提高效率。
假设检验方法(LRT-based)
我们前面提到过,对于高光谱目标检测问题,我们最先将其抽象为将一个待考察像素判定为目标或者非目标的二元假设检验问题,那么这个二元假设检验问题怎么去设置呢?文中给出了这样的设置方法:
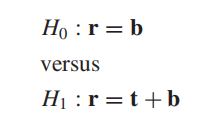
其中,H0就代表了没有目标的情况,H1就代表了有目标的情况,b代表表示背景的向量,t代表表示目标的向量,他们都是L维的。当t已知时,这就是一个先验目标检测问题。
成功抽象出问题后,下面作者开始论述三种不同的情况下假设检验方法。
纯像素目标检测
纯像素目标检测就是最标准也是最基础的目标检测,刚好可以用我们上面那组公式给出的二元假设检验来描述,即目标的知识全部都是已知的。纯像素目标检测问题的像素全部都是真实非经加工的且只有一种类型光谱。
那么我们已经将问题抽象出来后如何进行检测呢?这就需要用到检测器:
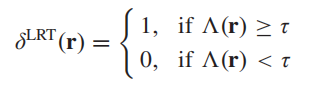
这里用的是似然比检验,其中
Λ
(
r
)
=
p
1
(
r
)
p
0
(
r
)
=
P
(
r
∣
H
1
)
P
(
r
∣
H
0
)
\Lambda(r)=\frac{p_1(r)}{p_0(r)}=\frac{P(r|H_1)}{P(r|H_0)}
Λ(r)=p0(r)p1(r)=P(r∣H0)P(r∣H1)为似然比(原文实际上是p0/p1,但个人认为这个地方原文写错了,因此改正),阈值定义为
τ
=
(
c
10
−
c
00
)
P
(
H
0
)
(
c
01
−
c
11
)
P
(
H
1
)
\tau=\frac{(c_{10}-c_{00})P(H_0)}{(c_{01}-c_{11})P(H_1)}
τ=(c01−c11)P(H1)(c10−c00)P(H0),这是一个由先验概率和代价因子决定的常数。
这里的一系列c都是代价因子,如
c
10
c_{10}
c10代表实际假设为H0时而判决为H1的代价。
我们观察似然比的定义,显然
p
0
(
r
)
p_0(r)
p0(r)与
p
1
(
r
)
p_1(r)
p1(r)都是需要我们提前知道的,但是显然r是包含着背景信息b的,因此如果想获得r的概率密度分布,我们就必须要预先知道背景b的概率密度分布。于是这里就对背景b的概率分布做了假设,假设其为矩阵为
μ
b
\mu_b
μb、协方差为K的高斯分布,因此有:
p
0
(
r
)
=
e
x
p
(
−
1
2
(
r
−
μ
b
)
T
K
−
1
(
r
−
μ
b
)
)
p_0(r)=exp(-\frac{1}{2}(r-\mu_b)^{T}K^{-1}(r-\mu_b))
p0(r)=exp(−21(r−μb)TK−1(r−μb))
p
1
(
r
)
=
e
x
p
(
−
1
2
(
r
−
μ
b
−
t
)
T
K
−
1
(
r
−
μ
b
−
t
)
)
p_1(r)=exp(-\frac{1}{2}(r-\mu_b-t)^{T}K^{-1}(r-\mu_b-t))
p1(r)=exp(−21(r−μb−t)TK−1(r−μb−t))
那么就有:
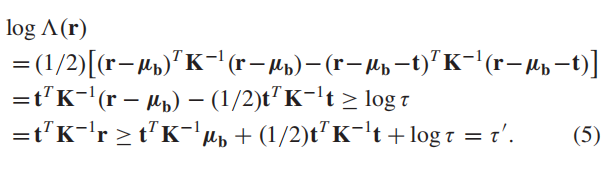
于是我们的检测函数就可以简化为:
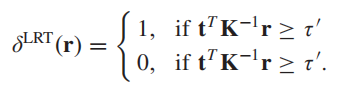
之后作者还给出了一个此时最大信噪比的计算方式:
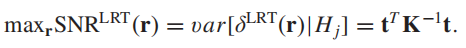
我们知道信噪比应该等于信号与噪声的功率谱之比,但通常功率谱难以计算,有一种方法可以近似估计图像信噪比,即采用信号与噪声的方差之比,即:
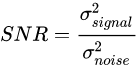
因此这里为了求解信噪比去计算了方差(var),我们也可以看出,这里的信噪比实际上是一个常数,仅与目标向量特征和背景协方差特征有关。
亚像素(超像素)目标检测
当然我们知道,实际中的高光谱图像不可能百分之百是纯像素的,可能由于器件精度不够能原因,导致像素排列并不是全部都是由原始拍照结果得来的,有些像素可能是按照某种方法填充上的。这种,我们一般称之为亚像素(这时整理总结的百度上的定义,没有找到更科学地说明)。
这种情况下我们需要对二元假设检验问题的数学模型做一点改动:
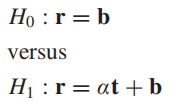
这里实际上只多了一个
α
\alpha
α,这就是所谓的丰度分数(abundance fraction),实际上是一个未知的、需要估计的表征目标信号强度的参数。如果按照这个观点来看,实际上,我们前面的纯像素目标检测的情况也只不过是让
α
\alpha
α取1了而已。
要解上述的假设检验问题,需要用到广义似然比检验GLRT:
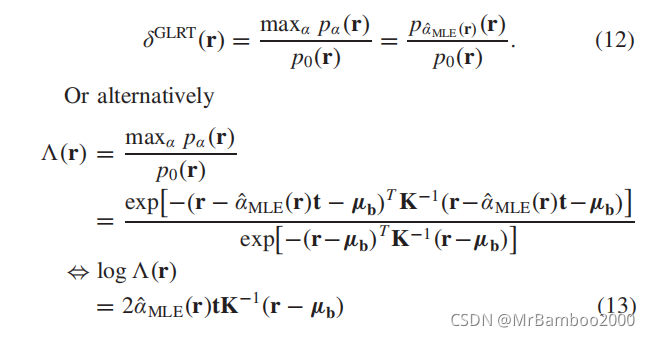
可以看出此时仍然假设了背景b为高斯分布。这时候还需要计算参数
α
^
M
L
E
(
r
)
\hat{\alpha}_{MLE}(r)
α^MLE(r)。
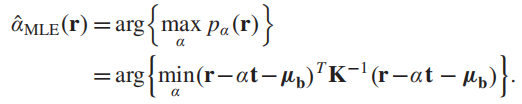
a
r
g
{
m
a
x
α
p
α
(
r
)
}
arg\{max_{\alpha} p_{\alpha}(r)\}
arg{maxαpα(r)}应当是表示在
p
α
(
r
)
p_\alpha(r)
pα(r)取最大值时,此时
α
\alpha
α的取值,因为这用的是高斯分布表示(exp函数里面有负号),因此就等价为了下面取最小值时的情况。
那么要求这个
α
\alpha
α值也很简单,只需要对
α
\alpha
α求偏导另偏导为0就可以了,即:
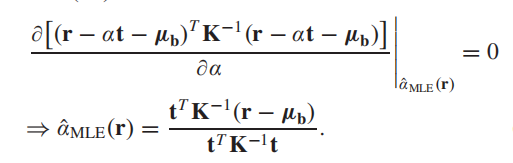
然后我们再把这个
α
^
M
L
E
(
r
)
\hat{\alpha}_{MLE}(r)
α^MLE(r)参数带到纯像素部分那种形式的检测器函数中,有:
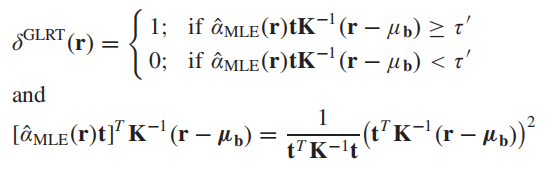
在这种情况下,信噪比可以表示为:
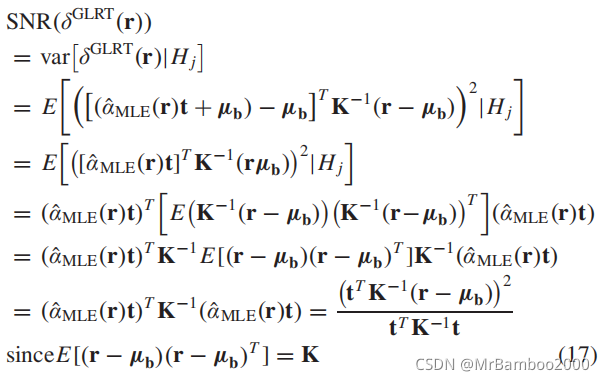
这时我们可以发现这个信噪比不再是一个常数,这是因为
α
^
M
L
E
(
r
)
\hat{\alpha}_{MLE}(r)
α^MLE(r)参数需要从r中得到。而且非常有趣的一点是,这个SNR检测器与LTR检测器完全一致,这也说明了基于假设检验的LTR方法与基于SNR的方法是有很大程度上的联系的。
混合像素目标检测
除了上述情况外,还有一种情况叫混合像素目标检测,即像素包含不同类型的光谱,而目标检测只包含其中一部分类型。
这时候我们要再对抽象出来的假设检验模型进行改动:
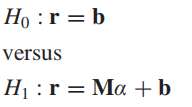
这里
M
=
[
t
1
,
t
2
,
.
.
,
t
p
]
M=[t_1,t_2,..,t_p]
M=[t1,t2,..,tp],
α
=
(
α
1
,
α
2
,
.
.
.
,
α
p
)
T
\alpha=(\alpha_1,\alpha_2,...,\alpha_p)^T
α=(α1,α2,...,αp)T,也就是说,相比于上一部分,这个改动实际上就是从一种类型的目标特征扩展到了多种类型,丰度分数也随之扩展到每一种类型对应一个。因此,
M
α
M\alpha
Mα就可以看作是混合像素的目标。
那么怎么解这个假设检验问题呢?我们可以把这个模型做一下简化,往上面两种方法上靠。文中给出的方法是用OSP(正交子空间投影)方法去求解。我们的目标是在M的一组t中找出感兴趣的t,也就是说我们需要在r中消除不期望的
t
1
,
t
2
,
.
.
.
,
t
p
−
1
t_1,t_2,...,t_{p-1}
t1,t2,...,tp−1这一系列信号,然后对期望的
t
p
t_p
tp信号进行检测。这时我们定义一个正交子空间投影器来完成投影,消除干扰信号:
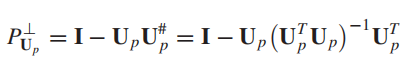
因此,做了投影之后的假设检验模型变为:
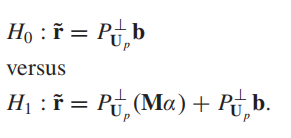
为了和上一部分达成形式上的统一,我们做了如下处理:
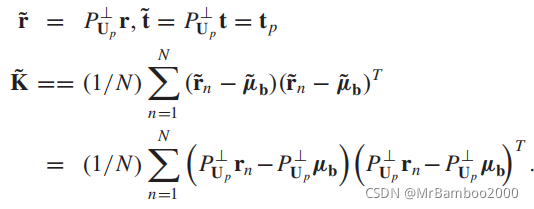
这样假设检验的模型就与上面相同:
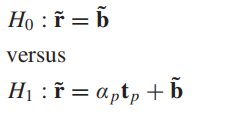
后面的LRT检测器的构造以及SNR的计算也和上面相同了,这里就不再展开讲了,直接看下面的结果:
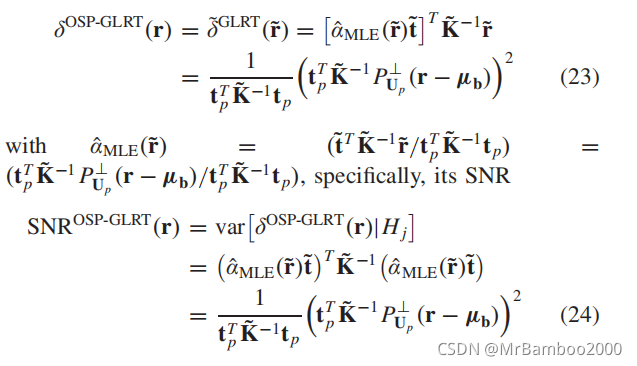
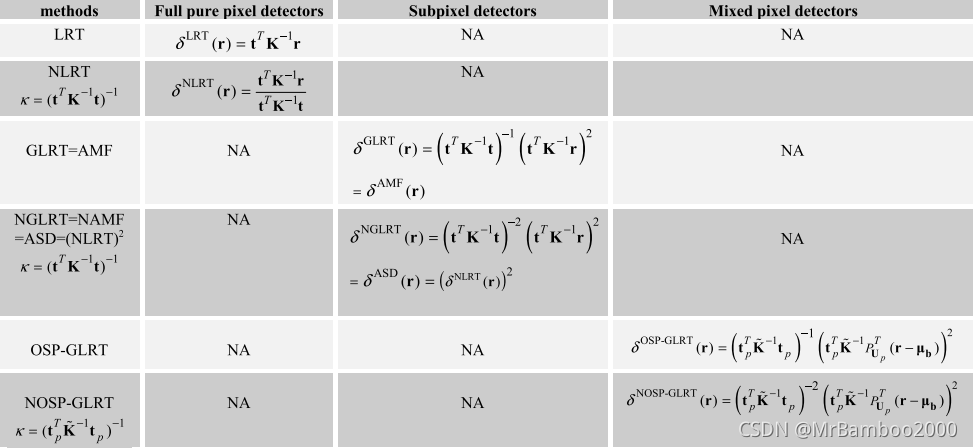
这样我们的基于假设检验的LRT模型就结束了,这里作者对不同的图像类型在模型的形式上进行了统一,让整个理论体系变得非常的清楚。我们可以归纳出一个解法思路:
首先列出二元假设检验模型,然后计算丰度分数(如果有)、似然比和阈值,最后进行检测。
本节的精华都在下面这个表中:

基于信噪比的检测方法
在前面的方法中,我们可以发现一个问题,那就是表示背景b的概率分布都是我们假设出来的,也就是全都无差别的设成了高斯分布。但是在实际情况中,不一定所有的背景都可以表示为高斯分布。因此,我们需要探寻一种方法,无需做出一些先验的概率分布假设。因此,作者提出了基于信噪比的假设检验方法,这种方法只需要简单知道一些一阶二阶统计量,就可以进行检测。
其实从我个人角度来说,基于信噪比的检测这个思路可能更易于想到。作为一个没有接触过高光谱目标检测的人,我首先想到的方法就是在通信和信号处理领域大名鼎鼎的匹配滤波器,即设计一种滤波器,使得当其输入信号具有某一特殊特征时,其输出信噪比达到最大。这也就是信噪比检测的基本思想。
从这个角度出发,我们可以得到其最基本的检测器模型为:
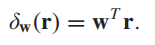
其中w本质上就是一个FIR滤波器。下面我们就来看作者是如何从SNR出发重新推导LRT、GLRT以及OSP-GLRT。
纯像素目标检测
在高光谱目标检测中,背景可以由由协方差矩阵K来表示的。因此在前面的LRT检测器中,总存在
K
−
1
K^{-1}
K−1项来消除掉背景的影响。那么基于这个想法,作者提出了三种数据白化方式来处理掉一些统计特征以此来消除背景的影响。SNR检测器就是建立在这三种不同的数据白化方式上的。
DS空间中的数据白化
DS白化实质上是在原始数据空间中消除掉第一阶和第二阶的统计量。对于这种消除方式,我们可以很自然的想到归一化操作,而实际上DS白化也是这么做的:

那么因此,我们的检测器模型就可以换为:
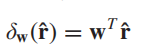
进而SNR就可以表示为:
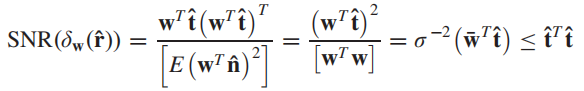
这就是非常典型的信噪比的基础定义,即信息能量与噪声能量之比。分子上因为两个向量一个为1×L维一个为L×1维因此乘起来是一个数,所以可以直接写作向量乘积的平方;而分母上则是用到了方差与期望的关系,即D(X)+(EX)2=E(X2),这里我们让噪声向量
n
^
\hat{n}
n^的均值
μ
b
\mu_b
μb设为0,方差
σ
2
\sigma^{2}
σ2设为1,因此下面就可以表示为
w
T
n
^
w^{T}\hat{n}
wTn^的方差,即wTw也就是||w||2。再后面一个等号后的
w
ˉ
=
w
∣
∣
w
∣
∣
\bar{w}=\frac{w}{||w||}
wˉ=∣∣w∣∣w,最后的不等式表明通过我们的滤波器后的信号的信噪比不大于目标的能量。
我们要使信噪比最大,而显然当不等式取等时信噪比最大。取等条件在前人的研究中出现过,即:
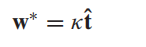
把这个w*代入SNR计算式,可得:
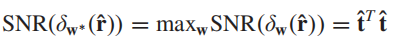
把w*代入SNR检测器模型,并把DS白化也代入,可以得到:
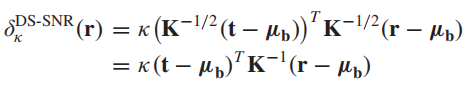
把DS白化带入上面的最大信噪比,得到:
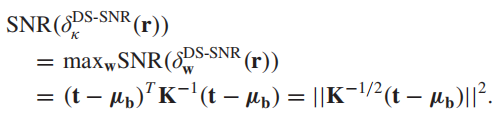
下面对这个
κ
\kappa
κ值做一些处理,当
κ
=
1
\kappa=1
κ=1时,得到:
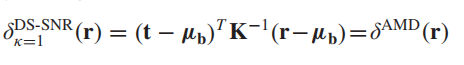
这个就相当于一个AMD(自适应匹配检测器)。
而让r=t,即让我们的检测样本就是目标时,有:
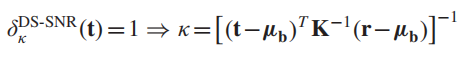
此时检测器为:
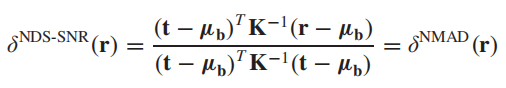
此时为一个NAMD(标准化AMD)。
K-空间中的数据白化
这里的白化方式是仅仅将在原始数据空间中表示背景的协方差矩阵消除掉,因此有如下变换:
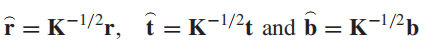
因此检测器模型变为:
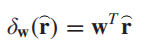
按照上面部分的推导方式,最终检测器和最大SNR为:
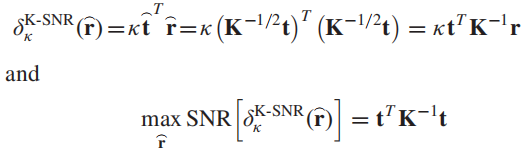
然后对
κ
\kappa
κ做处理,
κ
=
1
\kappa=1
κ=1时没有特殊的结果产生,略过。让r=t,有:
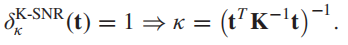
此时检测器可表示为:
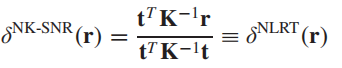
这时有趣的事情发生了,这就相当于一个标准化后的LRT检测器。
R-空间中的数据白化
这里的处理方法是消除原始数据空间中表示背景的相关矩阵。我们看到K-空间也好,R-空间也好,其都没有对一阶的统计量均值进行处理,在数据分布上来说,没有把数据全都分布到原点附近。
白化的变换为:
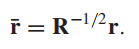
检测器模型变为:
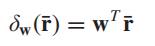
按照上面的推导方式:

最终检测器为:
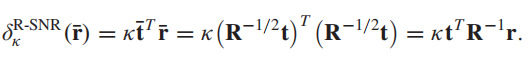
按上面方式分别处理
κ
\kappa
κ后,有:
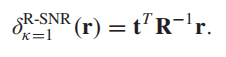
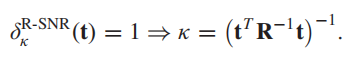
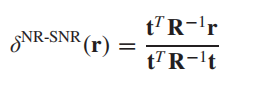
我们来看这个检测结果,它和之前高光谱目标检测中一个最著名的检测器CEM检测器一模一样,有关CEM检测器,网上资料较多,此处不再赘述:
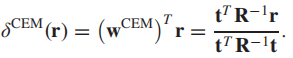
也就是说,CEM检测器实质上也是一种SNR检测器,且是一种在R-空间中被标准化后的SNR检测器。从原理上讲,CEM本质上也是用了匹配滤波器的思想,且利用的准则也与信号的能量有关。只不过CEM是在满足约束条件式的情况下滤波器的输出能量最小,而SNR方法通常是让输出信号的信噪比最大。
亚像素目标检测和混合像素目标检测
对亚像素目标检测来说,其相对于纯像素目标检测实际上只是多了一个参数丰度分数
α
\alpha
α,因此我们只需要估计出
α
\alpha
α再进行处理即可;而对于混合像素目标检测来说,其核心点在于正交子空间投影器这个预处理,因此我们只需要构造出合适的OSP再进行处理即可。
首先来看
α
\alpha
α的估计。
在LRT方法中,丰度分数
α
\alpha
α的估计靠的是MLE(极大似然估计),但是在SNR方法中,我们没有假设概率分布,因此也就无法使用MLE方法,这里取而代之的是使用了MD(马氏距离)作为估计方法。马氏距离是一种度量相似度的方法,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。马氏距离定义如下:
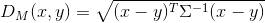
其中Σ是多维随机变量的协方差矩阵,如果协方差矩阵是单位向量,也就是各维度独立同分布,马氏距离就变成了欧氏距离。
于是,丰度分数
α
\alpha
α的计算方法如下:
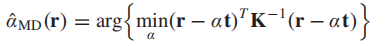
也就是说这里是找满足
r
r
r和
α
t
\alpha{t}
αt间距离最小,即相似性最高的
α
\alpha
α值。
那么其在DS空间中的信噪比就可以表示为:
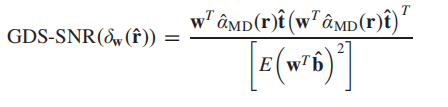
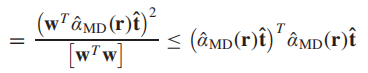
取等条件为:
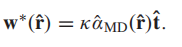
检测器就可以写作:
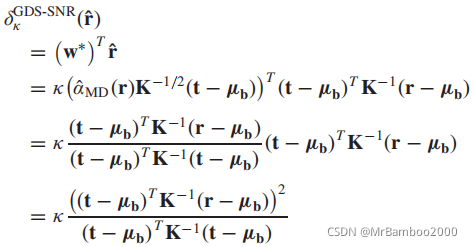
使
κ
=
1
\kappa=1
κ=1,有:
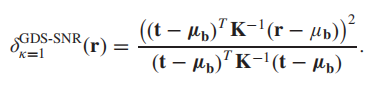
让检测器值为1,即r就是t,有:
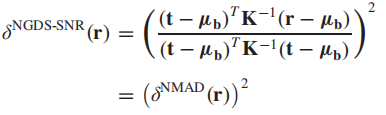
可以发现此时的检测器可以写作是一个NAMD检测器的平方。
K-空间和R-空间同理,推导过程不再赘述,但是我们可以看一下他们对
κ
\kappa
κ取特殊值时的结果。
(1)K-空间,
κ
=
1
\kappa=1
κ=1:
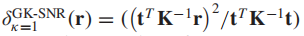
可以看出这就是一个AMF(自适应匹配滤波器),也就是和我们前面提到的GLRT形式基本一致。
(2)K-空间,检测器为1:
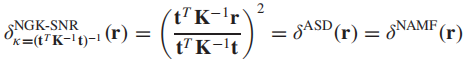
可以看出这时一个标准化后的AMF(NAMF),也可以叫做ASD——自适应子空间检测器。
(3)R-空间,检测器为1:
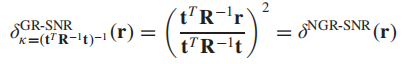
通过观察,我们发现这个结果是一个标准化后的亚像素R空间SNR检测器,但我们还可以发现其实际上也是前面提到过的CEM检测器的平方。
对于混合目标检测,我们实际上处理方法一样,只不过采用的是经过投影后的一系列变量,最后把投影器代入还原为原来空间的变量表示。文章只以K-空间为例作了简要说明:

最后做个总结,各类检测器如下表所示:

总的来说,基于SNR的检测方法无需假设概率分布,作者依托三种数据白化方式,在不同的任务中分别推出各种检测器,并于前人的研究相结合,讲前人的研究成果在SNR检测器中进行了分类,完成了理论的统一,观感十分舒适。
LRT检测与SNR检测的关系
我们在前面提到过,在我们用LRT检测器去算SNR检测器时,其结果与LRT检测器完全相同;而我们在对SNR检测器的参数
κ
\kappa
κ做处理后,其得到的结果也与LRT检测器有很大的相似性。因此我们可以看出,SNR方法和LRT方法是有一定的相通性的。
具体表现在如下表中:

文中作者还做了一个很有意思的操作,那就是用我们之前提到过的正交子空间投影器去重新表示了SNR检测器,这个推导非常优美,暂且记录一下:
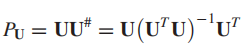

如上推导是用了一个投影的算子和K-空间白化后的变量去表示了一个GK-SNR检测器,即
κ
=
1
\kappa=1
κ=1的K-空间亚像素目标检测的检测器。可以看到最后的结果只由一个包含了K-空间白化后变量
t
⌢
\overset{\frown} {t}
t⌢的投影算子
P
t
⌢
P_{\overset{\frown} {t}}
Pt⌢和一个K-空间白化后的变量
r
⌢
\overset{\frown} {r}
r⌢。
同理,也可以推导出:
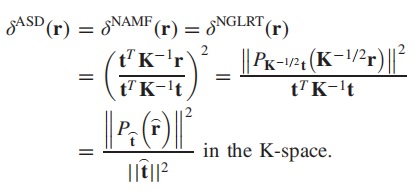
观察这个形式,就可以证明让检测器为1时,确实相当于对检测器做了一个标准化,所以可以将这种情况下的
κ
\kappa
κ代入检测器后获得检测器的标准化形式。
因此可以重新扩展LRT方法为:
基于SA(光谱角)的检测方法
我们知道,基于SNR方法的基本思想是匹配滤波,但是在SNR方法中,我们所用的滤波器是线性的。而在某些情况下,线性滤波器不一定能达到最优的效果,因此就需要设计非线性滤波器。那么在高光谱目标检测这个背景下,最简单的非线性滤波器莫过于去测量两个光谱向量之间的角度如何,根据角度进行检测,因此就有了SA检测器。
既然总的思想没变,还是匹配滤波,自然也不需要用到概率分布,且三种白化方式也需要被用以消除背景的影响。我们以K-空间为例,得到此时光谱角的定义如下:
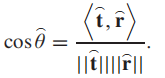
那么检测器就可以表示为:
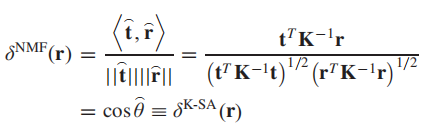
这个形式就是NMF(标准化匹配滤波)的形式。
对其做一个平方,可以得到:
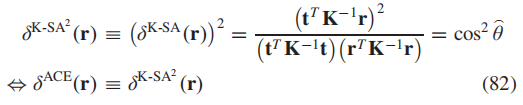
而这个形式也就是前人提出的ACE(自适应余弦估计)方法。
同理,我们把这个推导过程引入DS-空间和R-空间,有:
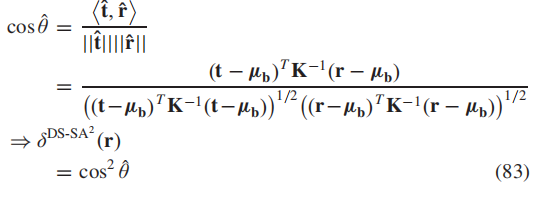

在这一部分我们又统一了两种前人提出的方法——NMF和ACE,并且给出了在其他两种白化方式下的新检测器,进行了理论体系的完备与统一。
三维ROC曲线
对于以往的高光谱目标检测问题,由于我们都是将其看作二元假设检验问题,因此其评估方式往往采用二维的ROC曲线。但经过我们上面的这一系列扩展后,仅仅用二维的ROC曲线去评估预测结果时,效果就不是很理想了。因此这里给出了一种新的、更有效的评估方式——三维ROC曲线。
我们知道,一般的二维的ROC曲线可以用来表征分类器的性能,其构造方式为横轴选FPR,即预测为真实际为假的概率,纵轴取TPR,即预测为真实际也为真的概率。我们通过计算这个曲线的面积,记为AUC,来衡量检测的性能。在我们实际的高光谱目标检测问题中是选了
P
D
P_D
PD和
P
F
P_F
PF来构建ROC曲线。两个概率分布定义如下:
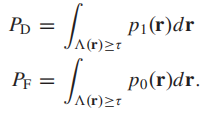
在这种状态下计算的AUC就记作AUC(D,F),但这个值存在着一些问题。首先我们知道,因为两个概率分布都是由同一个阈值
τ
\tau
τ计算而来的,所以当
P
D
P_D
PD和
P
F
P_F
PF很大时,AUC(D,F)值也很大,被判断为性能很好。但是实际上这个AUC(D,F)值并不能反应对背景的抑制能力,所以用其反应性能是不完备的。所以作者提出了用
P
D
P_D
PD、
P
F
P_F
PF和
τ
\tau
τ三个共同来表征性能。这就是三维ROC曲线的三个维度。
这样就会产生三个面
(
P
D
,
P
F
)
(P_D,P_F)
(PD,PF)、
(
P
D
,
τ
)
(P_D,\tau)
(PD,τ)以及
(
P
F
,
τ
)
(P_F,\tau)
(PF,τ)。分别可以作AUC值,分别表征二维ROC曲线性能、检测性能、以及背景抑制性能。我们也可以进一步定义如下指标用于检测,如下图所示,不再赘述:

总结
这篇文章是我在高光谱目标检测领域精读的第一篇文章,花了很长的时间去搞懂里面的推导与逻辑。这篇文章可以说是一个带有综述色彩的论文,其在总结前人理论的同时,又提出了一套全新的可以包含前人理论的框架,将这个领域变得更加体系化、条理化,让我这个初学者阅读时的观感非常舒适,既可以总览整个领域,又可以发现作者的新idea。
版权声明:本文为CSDN博主「MrBamboo2000」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_44226427/article/details/121411010









暂无评论