
参考https://blog.csdn.net/u012436149/article/details/69660214
https://blog.csdn.net/b1055077005/article/details/100152102
交叉熵损失(Cross Entropy loss)
交叉熵损失有多种形式:
(1)
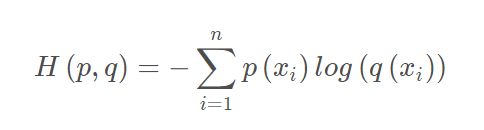
(2)
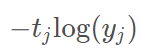
(3)
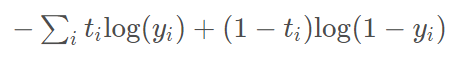
(4)
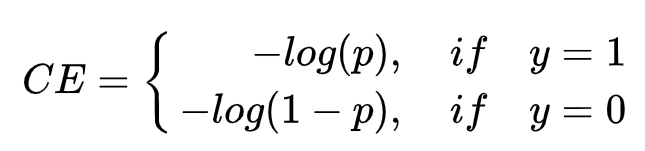
首先,这4种都是交叉熵,没有假的。
接下来我们看看这4种交叉熵是怎么得到的?
其实都是在(1)上面衍生得到的。
(1)
(1)是如何得到的参考https://blog.csdn.net/b1055077005/article/details/100152102,也是最好理解的。
交叉熵的目的就是希望判断两个概率分布的差异,交叉熵越大,则差异越大,用其作为Loss也合情合理。
对于(1)这个式子
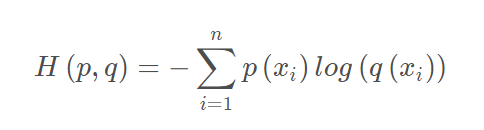
P是代表gt的分布,q代表预测的分布,i为类别,H(p, q)就是计算这两个分布对于每类的概率的差异
eg.

则计算交叉熵损失:
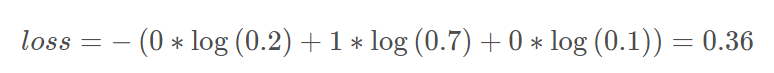
(2)
(2)其实就是(1)的一种特殊形式,因为一般来说,gt是确定的类别,如(1)中表所示,P(狗)的概率为1,其他都是0,就算按(1)的公式,算出来最后其实就是-P(狗)*log(q(狗))=-1xlog(0.7)=0.36
不过因为可能有label smooth等操作,P(猫)\P(马)可能并不为0,因此要按(1)的公式计算
(3)
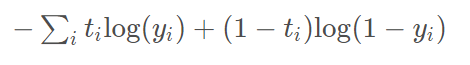
(3)主要与(2)对比,同时考虑并不只有gt类别为1的情况,(2)主要是针对最后一层为softmax层的结果,即所有类别的概率和为1,而(3)则针对Sigmoid层的结果,因为Sigmoid层出的结果,所有类别的概率和并不一定等于1,因此只能把每个样本对于每个类别的预测单独当成一个二分类样本,计算loss(BCE loss)(Binary Cross Entropy loss)
eg.
| * | 猫 | 狗 | 马 |
|---|---|---|---|
| GT | 0 | 1 | 0 |
| Predict | 0.2 | 0.8 | 0.4 |
此时对于猫的预测分布,gt=[0,1],predict=[0.2,0.8]
L
o
s
s
(
猫
)
=
−
(
0
∗
l
o
g
(
0.2
)
+
1
∗
l
o
g
(
0.8
)
)
Loss(猫)=-(0*log(0.2)+1*log(0.8))
Loss(猫)=−(0∗log(0.2)+1∗log(0.8))
这个样本的loss=loss(猫)+loss(狗)+loss(马),即(3)式
(4)
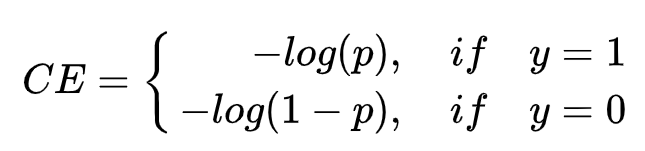
(4)其实与(3)的BCE loss是等价的
同时假设gt概率只有1和0,即假设gt概率是确定的(一般来说都是这样,不过其实也有特殊情况,比如CornerNet/CenterNet那种对gt做了高斯模糊的情况)
L
o
s
s
=
−
y
∗
l
o
g
(
p
)
−
(
1
−
y
)
∗
l
o
g
(
1
−
p
)
Loss=-y*log(p)-(1-y)*log(1-p)
Loss=−y∗log(p)−(1−y)∗log(1−p),令y=1即是(4)中的上半情况,令y=0则是(4)中的下半情况
Focal Loss
Focal loss的主要目的是抑制易分样本,平衡正负样本
(1)平衡正负样本
正负样本是BCE里的说法,对于
L
o
s
s
=
−
y
∗
l
o
g
(
p
)
−
(
1
−
y
)
∗
l
o
g
(
1
−
p
)
Loss=-y*log(p)-(1-y)*log(1-p)
Loss=−y∗log(p)−(1−y)∗log(1−p),gt(即y)=0则是负样本,y=1则是正样本,在目标检测中,anchor里总是负样本偏多,因此要抑制负样本,
=>
L
o
s
s
=
−
α
y
∗
l
o
g
(
p
)
−
(
1
−
α
)
(
1
−
y
)
∗
l
o
g
(
1
−
p
)
Loss=-\alpha y*log(p)-(1-\alpha)(1-y)*log(1-p)
Loss=−αy∗log(p)−(1−α)(1−y)∗log(1−p)
这跟普通的"两个loss分别加个系数来控制其比例"挺像的,
α
\alpha
α越大则负样本的loss越小
(2)抑制易分样本
如何定义易分样本?
=>易分样本=预测概率大的样本
因此拿预测概率做文章,把预测概率p作为系数加在其前面
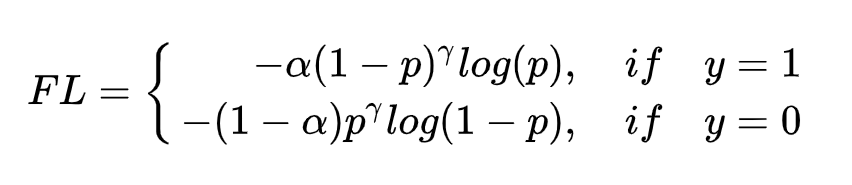
γ
\gamma
γ为一超参
如上式所示,预测概率p越大,且gt也为所预测的值(即y=1),则loss越小,p越小,且gt也为0(y=0),则loss也越小
0和1其实是两种类别,p代表预测为1的概率。总的来说,就是反正对应类别预测概率越高,且gt也对了,则loss越小
Focal Loss与目标检测
接下来看看Focal Loss是如何在目标检测中使用的?
以FCOS为例,看看目标检测分类分支的输出:
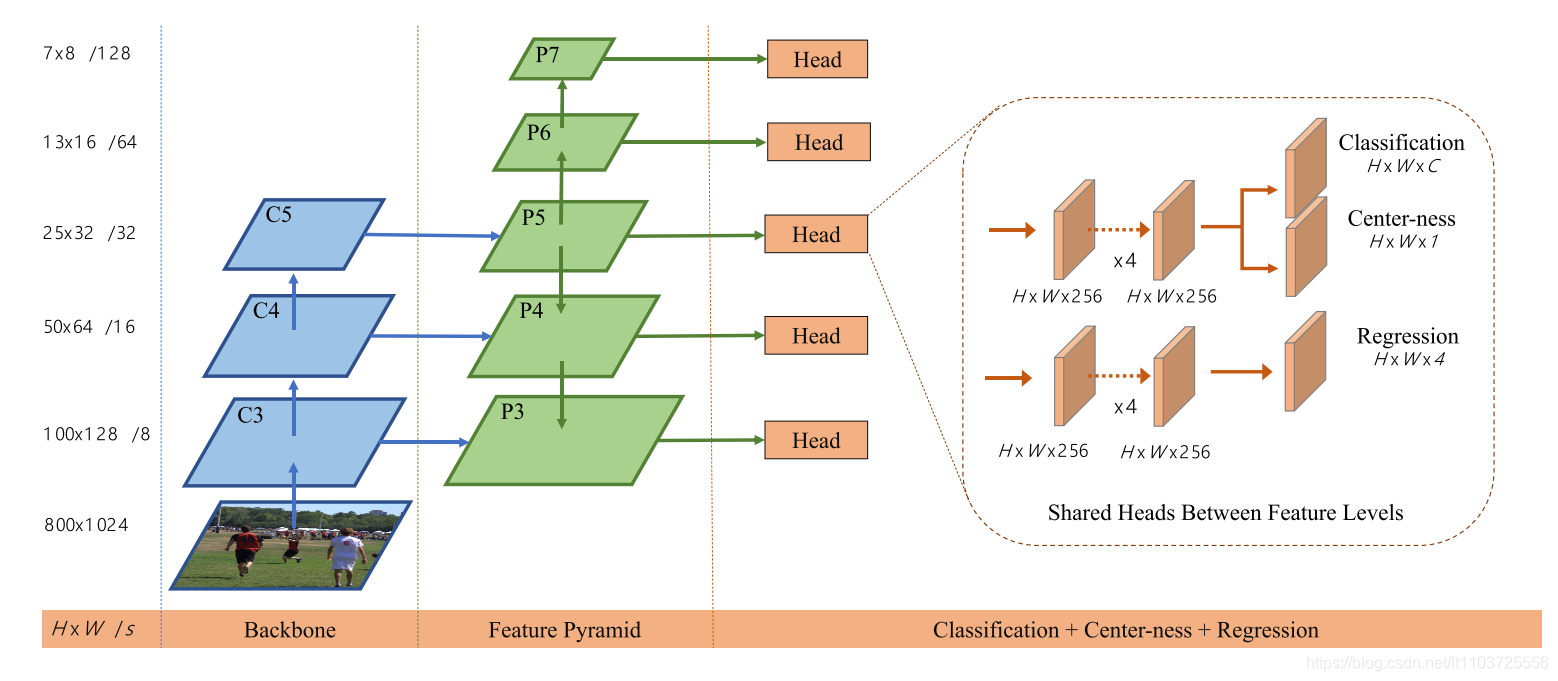
分类分支,输出维度为
H
∗
W
∗
C
H*W*C
H∗W∗C,C=类别数,也就是说,可以reshape为[H*W, class_num],即每个点对每个类别的概率,
[1] 第一行每个元素为第一个点对所有类别的概率[1, class_num]
》eg.class_num = 5, 第一个点的预测为[0.2, 0.4, 0.9, 0.1, 0.3]
》同时,target(gt)也为[H*W, class_num],表示所有点对应的gt类别(one-hot)
[2] 第一行每个元素为第一个点所被分配的gt框的类别的one-hot编码
(target分配及one-hot编码细节见末尾)
》eg.第一个点分配的gt为第3类,target的第一行为[0, 0, 1, 0, 0]
》eg.第一个点被认为是负样本,即没有对应gt,即被分为背景类(一般是第0类),target的第一行为[0, 0, 0, 0, 0]
以gt为第3类为例:
代码参考https://github.com/VectXmy/FCOS.Pytorch
| 302 def focal_loss_from_logits(preds,targets,gamma=2.0,alpha=0.25):
│ 303 ''' │ +giou_loss : function
│ 304 Args: │
│ 305 preds: [n,class_num] │ +iou_loss : function
│ 306 targets: [n,class_num]
│ 307 ''' │~
│ 309 preds=preds.sigmoid() │~
│ 310 pt=preds*targets+(1.0-preds)*(1.0-targets) │~
│ 311 w=alpha*targets+(1.0-alpha)*(1.0-targets) │~
│ 312 loss=-w*torch.pow((1.0-pt),gamma)*pt.log() │~
│ 313 return loss.sum()
首先对pred做sigmoid
由于做了sigmoid,所以是把每一类当做一个小样本算BCE,参考上面讲交叉熵损失的(4)的情况
上面的代码最终实现的是如下公式:
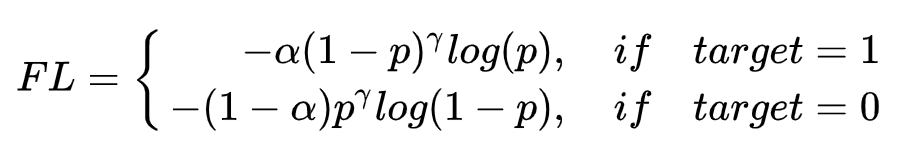
(1)
p
t
=
{
p
i
f
t
a
r
g
e
t
=
1
(
1
−
p
)
i
f
t
a
r
g
e
t
=
0
pt=\left\{\begin{matrix} p& if &target=1\\ (1-p)& if&target=0 \end{matrix}\right.
pt={p(1−p)ififtarget=1target=0
(2)
w
=
{
α
i
f
t
a
r
g
e
t
=
1
(
1
−
α
)
i
f
t
a
r
g
e
t
=
0
w=\left\{\begin{matrix} \alpha& if &target=1\\ (1-\alpha)& if&target=0 \end{matrix}\right.
w={α(1−α)ififtarget=1target=0
(3)
t
o
r
c
h
.
p
o
w
(
(
1
−
p
t
)
,
g
a
m
m
a
)
=
{
(
1
−
p
)
γ
i
f
t
a
r
g
e
t
=
1
p
γ
i
f
t
a
r
g
e
t
=
0
torch.pow((1-pt),gamma)=\left\{\begin{matrix} (1- p)^\gamma& if &target=1\\ p^\gamma& if&target=0 \end{matrix}\right.
torch.pow((1−pt),gamma)={(1−p)γpγififtarget=1target=0
(4)
w
∗
t
o
r
c
h
.
p
o
w
(
(
1.0
−
p
t
)
,
g
a
m
m
a
)
=
{
α
(
1
−
p
)
γ
i
f
t
a
r
g
e
t
=
1
(
1
−
α
)
p
γ
i
f
t
a
r
g
e
t
=
0
w*torch.pow((1.0-pt),gamma)=\left\{\begin{matrix} \alpha(1- p)^\gamma& if &target=1\\ (1-\alpha)p^\gamma& if&target=0 \end{matrix}\right.
w∗torch.pow((1.0−pt),gamma)={α(1−p)γ(1−α)pγififtarget=1target=0
(5)
p
t
.
l
o
g
(
)
=
{
l
o
g
(
p
)
i
f
t
a
r
g
e
t
=
1
l
o
g
(
1
−
p
)
i
f
t
a
r
g
e
t
=
0
pt.log()=\left\{\begin{matrix} log(p)& if &target=1\\ log(1-p)& if&target=0 \end{matrix}\right.
pt.log()={log(p)log(1−p)ififtarget=1target=0
(6)
l
o
s
s
=
−
(
4
)
∗
(
5
)
=
{
−
α
(
1
−
p
)
γ
l
o
g
(
p
)
i
f
t
a
r
g
e
t
=
1
−
(
1
−
α
)
p
γ
l
o
g
(
1
−
p
)
i
f
t
a
r
g
e
t
=
0
loss=-(4)*(5)=\left\{\begin{matrix} -\alpha(1- p)^\gamma log(p)& if &target=1\\ -(1-\alpha)p^\gamma log(1-p)& if&target=0 \end{matrix}\right.
loss=−(4)∗(5)={−α(1−p)γlog(p)−(1−α)pγlog(1−p)ififtarget=1target=0
Focal loss实现!
综上所述,
目标检测中的focal loss计算时,把每个点当成一个样本,得到这个样本对每个类别的预测概率分布,与one-hot形式的targets的分布计算loss
两个分布计算loss,由于pred做了sigmoid,于是采用(4)的公式,将每个类别当做一个小样本,单独做BCE loss(以BCE为基础的Focal loss),然偶将每个类的BCE loss相加。
最终,这一个Batch里,每个点的Loss相加,除以正样本数量算平均
更进一步地说,
目标检测中的分类loss计算,是把每个点对每个类别的预测当成一个样本,计算BCE loss,求和求平均
正负样本的概念
什么是正样本?什么是负样本?
(1)一般来说,正样本参与所有loss计算,负样本只参与分类loss计算
(2)正样本的target为某个gt框,负样本的target为0,类别为背景
正负样本均衡
在做正负样本平衡策略时,主要考虑的应该是分类loss,因为只有分类loss里会同时存在正负样本
但是计算分类loss时是把所有点的所有类别的预测当做一个样本,我们来看看正/负样本不均衡有什么影响
eg.2个正样本,2个负样本,5类
pred1: [0.1, 0.2, 0.8, 0.4, 0.4] target1:[0, 0, 1, 0, 0] loss1:[0.1539, 0.1810, 0.4181, 0.2454, 0.2454]
pred2: [0.9, 0.6, 0.2, 0.3, 0.5] target2:[1, 0, 0, 0, 0] loss2:[0.0071, 0.3244, 0.1810, 0.2114, 0.2831]
pred3: [0.6, 0.2, 0.3, 0.4, 0.6] target3:[0, 0, 0, 0, 0] loss3:[0.3244, 0.1810, 0.2114, 0.2454, 0.3244]
pred4: [0.1, 0.3, 0.1, 0.2, 0.4] target4:[0, 0, 0, 0, 0] loss4:[0.1539, 0.2114, 0.1539, 0.1810, 0.2454]
4个样本,实际上是20个二分类样本,其中2个对应的gt是1,其他都是0
以二分类来说,正样本:负样本=2:18,照理说就算前景类/背景类样本做了均衡,二分类loss这里仍旧是负样本偏多啊
回头再来看看Focal Loss
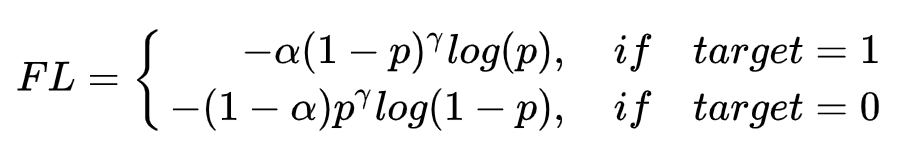
α
\alpha
α用于平衡正/负样本,应该指的是平衡target=1与target=0的样本,并不是前景类/背景类的anchor,而是每个anchor对不同类别的预测的二分类样本,中的正/负样本
一般来说
α
\alpha
α取0.25,也就是说,target=1的loss缩小为1/4,target=0的loss缩小为3/4
?
前面不是正样本的数量远少于负样本吗?为什么这里反而给正样本抑制了?
不明所以。
猜测是因为训练过程中正样本的loss往往比较大?。。
解:
不能单独只看
α
\alpha
α,还要看到
γ
\gamma
γ
γ
\gamma
γ是用来抑制易分样本的,易分样本的loss会被缩小

易
分
{
正
易
负
易
易分\left\{ \begin{matrix} 正易\\ 负易 \end{matrix}\right.
易分{正易负易
正易:target=1,且pred接近1
负易:target=0,且pred接近0
而target=0的样本是占绝大多数的,且其中大部分是背景且都是易分的,比如一张图片中,在训练一段时间后,大部分的背景anchor对所有类别的预测置信度都会接近0,因此被抑制。
由于target=0的loss被
γ
\gamma
γ抑制得太多,导致
α
\alpha
α要反过来加强target=0,抑制target=1
当然,以上为个人猜测。这两个超参的值也是Focal loss实验得出的。
根据实验,最佳超参:
γ
=
2
\gamma=2
γ=2,
α
=
0.25
\alpha=0.25
α=0.25
而当
γ
=
0
\gamma=0
γ=0时,
α
\alpha
α则应取0.75
补充:
(1)为什么最后是除以正样本数量,好像每个点都参与计算loss了啊?
我们来看看负样本的分类loss
eg.class_num = 5, 第一个点的预测为[0.2, 0.4, 0.9, 0.1, 0.3]
eg.第一个点被认为是负样本,即没有对应gt,即被分为背景类(一般是第0类),target的第一行为[0, 0, 0, 0, 0]
即:
preds=[0.2, 0.4, 0.1, 0.8, 0.2]
targets=[0, 0, 0, 0, 0]
代入Focal loss公式,全为Targets=0的情况
loss=1.1794
结论:确实正负样本都要计算loss且有值,但是最终只除以正样本的数量
至于为什么只除以正样本数,参考
轻松掌握 MMDetection 中常用算法(三):FCOS - OpenMMLab的文章 - 知乎
https://zhuanlan.zhihu.com/p/358056615
目的是平衡其他loss分支。个人理解是其他loss分支可能loss比较大?分类分支如果是除以所有样本了,loss就比较小了?
Mask:
shape为[batch_size, sum(_h*_w), 1]
与targets同样大小,mask的主要作用是计算正样本个数,正样本所在位置为True,负样本所在位置为False
计算每个batch中正样本的个数:
num_pos=torch.sum(mask,dim=[1,2]).clamp_(min=1).float()#[batch_size,]
Target
获取feature map上每个点对应的gt框
(1)对于每个level, 分别将feature map上的点映射回原图
(2)计算每个点对m个gt框的回归系数(m为这个batch内单张图片上gt数量的最大值)
(3)计算每个点到m个gt的center的距离
(4)计算每个回归框的面积
(5)根据策略计算每个点对应的gt
注意,这里的cls的gt可以是类别序号(1,2,3,4,5),不一定是one-hot,后面算loss的时候在前一步转one-hot就行
待补:
延申: segmentation中的Focal loss计算
版权声明:本文为CSDN博主「Rainylt」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/lt1103725556/article/details/115128523








暂无评论